在现代运筹优化与工程决策中，Gurobi作为全球领先的数学规划求解器，不仅具备卓越的线性与混合整数规划求解能力，还逐步涉足动态优化、非线性建模与嵌入式智能化应用等高阶领域。尤其在涉及时间阶段、状态转移和复杂约束结构的动态规划问题，以及具有非凸、非线性目标函数或约束条件的工程优化中，Gurobi正通过与算法结构的巧妙结合，为复杂系统建模提供稳定而高效的解决方案。本文围绕“Gurobi如何进行动态规划Gurobi如何处理非线性问题”两个关键主题展开系统阐述，并在第三部分延伸讲解“Gurobi如何建模多阶段多目标动态系统”的实际策略，帮助用户在多变条件下构建可行的数值优化框架。

　　一、Gurobi如何进行动态规划

　　动态规划（DynamicProgramming，简称DP）是一种分阶段递推的优化方法，核心思想是将复杂问题拆解为若干阶段子问题，并通过状态转移函数在各阶段之间递推最优解。然而，由于Gurobi本身是一个数值优化求解器而非算法框架，其不直接提供动态规划API，而是需通过构建“等价的数理规划模型”来间接实现动态优化。

　　1.动态规划问题的建模结构

　　-将动态规划中的“阶段”对应为决策时间点（如t=1,2,...,T）；

　　-每一阶段的“状态变量”与“决策变量”用Gurobi中的变量`addVar()`表示，通常需创建二维或三维变量矩阵：

　　-状态转移约束建模为线性等式或不等式，体现阶段间的依赖关系：

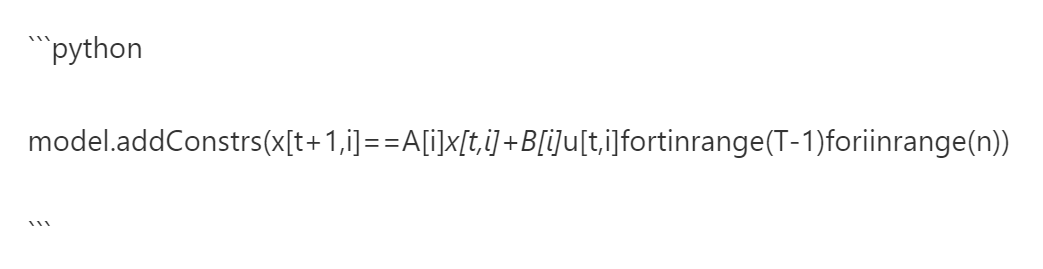
　　2.动态目标函数的分阶段构造

　　-多阶段目标函数通常表现为时间序列的加权和或折现值：

　　-若需考虑未来值的影响，可引入近似策略（如基于Bellman函数的线性近似）或时间窗滚动方式。

　　3.典型应用场景

　　-能源调度中的水库管理：将每一时刻的水位、流量作为状态变量，通过控制放水决策最大化电力收益；

　　-库存管理中的订购决策：在每一周期根据库存与需求状态决定订货量，目标为最小化总成本；

　　-金融资产配置中的再平衡策略：动态选择投资组合，使期望收益最大化或风险最小化。

　　4.滚动优化与近似动态编程（ADP）结合

　　-对于大规模动态问题，Gurobi可配合滚动时域（RollingHorizon）策略，每次仅求解一定窗口长度的子问题，提高实时性；

　　-使用近似策略值函数或策略迭代算法，实现学习型动态规划的求解框架。

　　5.建模技巧总结

　　-合理设置变量维度、统一索引命名，提升模型结构清晰度；

　　-使用Model.update()和Model.feasRelax()辅助调试不可行模型；

　　-将时间索引设为参数，避免硬编码以提高模型扩展性与复用性。

　　二、Gurobi如何处理非线性问题

　　非线性问题（NLP）广泛存在于资源配置、工业控制、金融分析等领域，包含非线性目标函数、非线性约束甚至整数与连续变量的混合形式（MINLP）。尽管Gurobi主打线性求解引擎，但也提供了对某些结构可解析非线性模型的支持，特别是在凸优化、二阶锥约束、二次规划（QP）等领域。

　　1.支持的非线性模型类型

　　-QP（QuadraticProgramming）：目标函数或部分约束为二次形式，Gurobi原生支持；

　　-QCP（QuadraticallyConstrainedProgram）：包含二次约束的模型，如二阶锥优化（SOCP）；

　　-MINLP（MixedIntegerNonlinearProgramming）：目标或约束为非线性表达式，含整数变量时需转为近似线性形式。

　　2.二次规划建模方式

　　-可使用`QuadExpr`表达目标函数或约束中的二次项：

　　```python

　　obj=QuadExpr()

　　obj+=0.5xQx+cx

　　model.setObjective(obj,GRB.MINIMIZE)

　　```

　　3.非线性问题的线性化策略

　　-对于不可直接表达的非线性项，如对数函数、幂函数、乘积函数，可使用PiecewiseLinearApproximation（PWL）进行线性逼近；

　　-亦可引入辅助变量+约束替代复杂函数，如`z=x*y`可转为McCormick包络线近似方式。

　　4.非线性可行域与求解策略

　　-Gurobi仅支持凸二次规划，若问题为非凸结构，需用户手动重构或转用其他求解器（如IPOPT、BARON）；

　　-对于复杂非线性结构建议：

　　-拆解为多个局部问题并分段求解；

　　-使用模型重构技术将非线性环节在Python外部处理后输入Gurobi求解核心部分。

　　5.性能优化建议

　　-减少二次项维度（如使用低秩近似）；

　　-使用`QCPDual`选项获得二阶约束对偶信息；

　　-合理设置模型容忍参数（如`OptimalityTol`、`FeasibilityTol`）确保结果稳定。

　　三、Gurobi如何建模多阶段多目标动态系统？

　　在智能制造调度、多周期投资决策、绿色能源配置等场景中，往往既涉及跨时间阶段的动态策略，又存在多维度优化目标如“效益最大化+能耗最小化”并存的问题，构成了多目标动态优化问题。

　　1.变量建模方式

　　-定义多阶段变量矩阵`x[t,i]`、`y[t,j]`等，分别表示不同阶段下的策略组合；

　　-每个目标函数分别以独立表达式构建：

　　obj1=gp.quicksum(cost[t]*x[t]fortinT)

　　obj2=gp.quicksum(emission[t]*x[t]fortinT)

　　2.多目标设定方法

　　-使用`model.setObjectiveN()`按优先级设置目标函数：

　　model.setObjectiveN(obj1,index=0,priority=2)

　　model.setObjectiveN(obj2,index=1,priority=1)

　　3.状态转移与目标约束协调

　　-引入动态转移约束，确保目标函数间逻辑一致，如成本目标依赖资源状态、碳排放目标依赖设备启停状态。

　　4.目标函数冲突的调解方法

　　-设置目标函数的最大容忍度`RelTol`平衡不同目标间的最优性与可行性；

　　-或引入“ε-约束法”，将一个目标转为约束条件，如“在成本不超过X的前提下最小排放”。

　　5.多目标动态建模的系统性建议

　　-使用外部配置文件定义目标函数权重与阶段窗口，提升模型灵活性；

　　-与数据平台接口集成，通过API调用实时数据构建动态目标函数；

　　-构建多解输出机制，为决策者提供多个可行策略集（非单一最优解）。

　　总结

　　通过对“Gurobi如何进行动态规划Gurobi如何处理非线性问题”的系统剖析，可以看出，Gurobi尽管起初为线性规划引擎，但在通过结构建模、函数转换与策略封装等方式的配合下，已具备求解高度动态化、复杂化、非线性化模型的能力。其在多阶段动态建模、目标函数多维化、状态演化建模等方向的延展潜力，为未来智慧制造、供应链优化与数字化决策提供了坚实支撑。随着高性能计算平台、AI辅助建模工具与云端求解技术的成熟，Gurobi的角色也将从求解器向“全流程优化平台”演进，成为数字决策链路中的中枢引擎。